.
~ building a tuned guitar ~
~ how the pitches 'E and G' core the building and tuning of a modern equal temper pitched guitar and bass ~
|
In a nutshell. Our modern, standard tuned guitars and basses today are built and tuned up around the 'E' and 'G' notes, letter name pitches etc. So no real surprise that songs and their styles when played in these keys sound super strong with a guitar or bass. The deep deep blues and rock love the open strings with their long sustainability, thundering bass etc. There's a million riffs in these open strings 'E' and 'G' and from 'A' and 'D' too for that matter :) Super clear that the top four pitches of the open strings give us the essential banjo leaning superbright rockabilly 'G 6' sounds. And thinking from the open low 'E' brings us 'Em 7', setting up all things leaning minor including modes and all blues' hue magics. All through this e-primer, the evolution of guitar chops from root blues to jazz are based in 'E' and 'G.' All theory studies in 'C', as in jazz blues studies. With a focus on 'movable shapes' for scales and chords, all 12 paired keys can blossom towards the bebopper's palette, an 'anything from anywhere' local universe at all the frets up and down the neck. |
The modal nutshell. Knowing that the modes hold the original pitches that are still creating our melodies of today, we could easily lean a bit deeper towards the musical realms of the legends through our histories; knowing that a melody made from the pitches of a mode today can carry all of its historical energies and meanings, carry its nuances and powers, that ties the artist into the universal energies to channel; and bring forth today the timeless quality and share with their listeners. So in theory, if today's relative major 'G and E minor' pairing of pitches / letter names; which we as the Ionian (G major) and Aeolian (E minor) modes, have that 'built in' richness of sonority an any guitar, then it follows that melodies created in the 'A' Dorian mode, or 'B' Phrygian, 'C' Lydian, 'D' Mixolydian and 'F#' Locrian can have the extra 'built in' deeper sonority on a guitar too, we each just have to find it. |
Modern tuning ways. We take the general term 'tuning' a couple of directions in the following discussions. There's the basics of how our guitars are physically built up so as to play 'in tune.' This concerns the theory of how the frets are located and the pattern of markers found on a modern guitar fingerboard. So looking to answer the 'why' do the frets get smaller as we ascend, what pitches, keys and modes are built into our guitars with standard tuning and basses, and how it all stays in tune through the 12 major and minor key centers. There's a how to tune up a six string guitar or four string bass from a tuning fork start point and then three open tunings common in today's musics. First, the math :) |
Building a modern tuned Americana guitar. Our modern builders of today have a fairly solid 200 years or so of instruments to examine and study to bring forth the modern marvels of today. Electronic wizardry aside, we've a rather remarkable acoustic instrument today capable of melodies, arpeggios, chords, rhythms, blue notes; a fully chromatic aural spectrum of possibilities. |
Going back even a bit before the guitar to the lute and vihuela, whose 'rule of 18' fret mathematics creates a fret location scheme capable of building an equal temper tuning into any style of fixed fret instrument, we find an evolving artistic refinement that continues today. |
 |
Our instruments become more accurate over the centuries as the math and tools used to physically locate frets on a piece of fretboard wood improved, thus the intonation of our instruments could also evolve. This gradual physical honing of the instrument's pitches into equal temper fret spacing surely plays a part in that it allows and encourages the evolution of harmony in the American jazz story. This evolution is surely traceable while moving through the decades of our American music history. That pitch doubling in chords is easier to tune than getting the multi-noted Hollywood chords, rich in the color tones, to sound good and in tune all improves on better crafted instruments. |
Regardless of how well crafted and in tune an instrument is, generally speaking the fret spacing scheme built into any guitar nowadays is an equal temper layout, which allows us to create all of our intervals, scales, arpeggios, our various chords and pitch clusters, from each of the 12 pitches of the chromatic scale. This marvelous tonal and musical dexterity has the distinctive title here of 'anything from anywhere', which even just as a one page treatise will, in theory, open up a nice new universe of possibilities. |
Anything from anywhere simply implies that all of our musical sounds and components can be equally created from any of the 12 pitches over the entire range of the instrument. And as we'll see as we progress in this study, our ability to slide our numeric pitch style indicator seamlessly through our popular musical styles is made possible by this pure equality of the 12 pitches. |
For today we think little of changing keys, moving ideas chromatically, further extending arpeggios beyond a tonal center, we even can stack complete tonal centers on top of one another and still sound in tune. Advanced musicians often will spontaneously transpose written music on sight to better accommodate a melody to a unique performance setting; a person's vocal range, instrumentation etc. Sky's the limit. Acquiring and strengthening these skills over the decades become solid intellectual challenges for the career musician, keeps the noodle engaged and in business. |
So as we evolve through our musical styles and count up the gradually increasing number of pitches employed, knowing that the structural basis of equal temper tuning provides these artistic resources, could very well provide the intellectual basis for further evolution of our musical resources thus the art it might create. Along this line of thought, we can ride a sequenced arpeggio to get there. |
The problem to be solved. Ever wonder why the width between the frets on our guitars, and most other fretted instruments, gradually gets smaller as we ascend in pitch? As pitch is determined by frequency of vibration, measured in cycles per second, it is our fret placement that properly divides up our string length, thus creating the different vibrations whence our pitches. |
What is needed for equal tempered fret spacing to work is a way to divide the octave into 12 equal parts or semitones (half steps) while realizing that our numerical cycles per second doubles in number from our root pitch to the octave pitch above it. Somehow we must convert the different pitches into the physically measurable spacing on the guitar fingerboard. |
|
So if the distance from A(4) 220 Hz to A(5) 440 Hz is one octave, we're multiplying 220 Hz times two to get 440 Hz. To divide that octave into twelve equal pitch increments, we need to use that number which, when multiplied by itself twelve times, equals two. In math parlay that number is the 'twelfth root of two.' (1) |
The early solutionist. We can trace the solution of this problem by taking the wayback machine some 450 years to the later Renaissance era of Florence, Italy. Here we find Vincenzo Galilei (1529-1591), father of famous astronomer Galileo. Written historical records reveal to us that Papa Galilei's main musical instrument was the lute and that he was an accomplished performer and noted composer. While movable frets were not uncommon in this era, Vincenzio preferred fixed, parallel frets which would produce a consistent intonation over the range of his instrument. Fixed, parallel frets ... seems awfully familiar doesn't it? (3) |
To tune such an instrument, Mr. Galilei is associated with the 'rule of 18', the first written mention of which is in his instructional text for lute. So named for the number used to divide a string length i.e., the distance from nut to bridge, the 'rule of 18' mathematics produces the division of the octave into the 12 half step pitches of equal temper tuning. Interesting to note that keyboard builders, tuners and players would continue to grapple with the same tuning issues for another century and a half or so before accepting and arriving at an equal temper equilibrium in tuning. And they needed this to tune a fully capable piano, go figure. (4) |
While we can trace our guitar ancestors all the way back to the 12 century Moors of the Iberian Peninsula, and our modern version of the classical guitar to the early 19th century Spain, we have in essence used the rule of 18 to create the fret spacing to equal temper tune the pitches of any of the stringed instruments with fixed, parallel frets. (5) And in some parts of the world it is probably still in use today. |
'rule of 18' |
Application of the rule. This 'rule of 18' places the first fret of a fingerboard 1/18th from the nut, of the total length of the string. The second fret is located 1/18th of the remaining distance plus the distance to the first fret. We consistently measure each fret from the fixed string 'nut' to minimize errors. Do remember that we still have to saw a groove into the fingerboard and hammer in the metal fret. We simply repeat this process for the number of frets we need. Today, with the better calculating, measuring and building resources, the more refined and accurate figure of 17.817 is used for equal temper fret placement and is derived from the math associated with the pure mathematics solution of the 12th root of 2. |
This factor of 17.817 is used to calculate the 12 fret locations between the two pitches of the octave. It will work for any scale length and any number of pitches (frets) we need. Here is the formula to find the location of our 1st fret and the math that creates this 17.817 fret spacing constant. We'll examine the numbers associated with a 25.5 inch scale length of string and use the solution of the 12th root of 2 as 1.0594631. |
| 1) Scale length ( 25.5" ) divided by 1.0594631 = 24.0688" |
| 2) Scale length ( 25.5" ) - 24.0688" = 1.4312", the distance from the nut to the first fret. |
| 3) Scale length ( 25.5" ) divided by 1.4312" = 17.817", our fret spacing constant. |
| 4) Finding the placement of the 2nd fret, we now can use the spacing constant divided into our shortened scale length. Thus; 24.0688" divided by 17.817" = 1.351", to this we add our first fret spacing of 1.4312" to get 2.2782", our second fret is located 2.782" from the nut. Cool? |
| 5) Third fret: 25.5" - 2.782" = 22.718" / 17.817 = 1.275" + 2.782" = 4.057" |
| 6) Fourth fret: 25.5" - 4.057" = 21.443" / 17.817 = 1.203" + 4.057" = 5.261" |
| 7) Fifth fret: 25.5" - 5.261" = 20.239" / 17.817 = 1.135" + 5.261" = 6.397" |
| 8) Six fret: 25.5" - 6.397" = 19.103" / 17.817 = 1.072" + 6.397" = 7.469" |
| 9) Seventh fret: 25.5" - 7.469" = 18.031" / 17.817 = 1.012" + 7.469" = 8.481" |
| 10) Eighth fret: 25.5" - 8.481" = 17.019" / 17.817 = 0.995" + 8.481" = 9.436" |
| 11) Ninth fret: 25.5" - 9.436" = 16.064" / 17.817 = 0.901" + 9.436" = 10.338" |
| 12) Tenth fret: 25.5" - 10.338" = 15.162" / 17.817 = 0.8510" + 10.338" = 11.189" |
| 13) Eleventh fret: 25.5" - 11.189" = 14.311" / 17.817 = 0.803" + 11.189" = 11.992" |
| 14) Twelfth fret: 25.5" - 11.992" = 13.508" / 17.817 = 0.758" + 11.992" = 12.750" |
Each of the above calculations work with the full scale length to find the distance from the nut to each of the frets. In theory, builders measure each successive fret from the nut, as opposed from the bridge, to minimize goof ups. Having to measure the smaller distance apparently creates a greater accuracy. The octave at the 12 fret, being one half of the string length, provides a reset point of perfect clarity for the frets above #12. |
So at some point get your ax and a tape measure and see what you come up with. Having never personally built and fretted a fingerboard, I honestly do not know the difficulty. For purposes here, we simply need to recreate the math for our own edification. This understanding forms the core basis of how our tuning is created and built into our instruments, creating the foundation for our music theory discussions. |
The dots. In writing this, multiple queries revealed a continual mystery as to why the dots / fretmarkers are located where they are on the neck of our modern guitars. Looking at available pictures of older guitars from various sources, there is some variability in placements. Some cats even add additional dots for super lightning quick references. So thinking of what was the oldest song we have that is consistently found in modern collections written in the same key centers, and upon examining the instruments I had at the time, the following solution occurred to me. The English song "Geensleeves" takes us back near the mid 1550's or so before our six string guitars really got their start. Modern scoring of the song finds it mostly centered in the key of E minor with the bridge / refrain going to G major. So in looking at the fret markers on my guitars, the corresponding pitches create E Dorian and G Lydian. In today's theory, these are parented by the D Ionian / D diatonic major scale. While even the lutes of this era are said to be equal temper tuned, thanks to their fret placement by the rule of 18', good chance that the modal system of pitch organization still ruled the day. Am I way out of my league here? Absolutely, but who doesn't love a good mystery :) Here's a picture of the first octave of my old guitar. |
|
open E |
3rd / G |
5th / A |
7th / B |
9th / C# |
12th / E |
 |
|
Musical styles / tunings. Do we tune our instruments different ways depending on musical style? In some cases we surely do. Early blues players used open G tuning carried over from the banjo. Slide guitar players often lean towards the open tunings. Singers will often open tune their axe's as it can free up their voice to find different nuances with pitch. For example, there's three G's in the open G major chord commonly used by singer/guitarists, so not a lot of wiggle pitchwise, (not being a singer I really shouldn't say.) A best example of voice / open tunings just might be in Joni Mitchell's work. Another might be in Bob Dylan's work, where his natural tone of voice, its expression and inflection, easily overcomes any pitch dominance created by the standard tuning he usually chose for his acoustic git. |
Old becomes the new new. The open 'G' tuning, goes way deep deep deep into our American musical roots. First as a banjo tuning then in its adaption to the guitar, as used by our turn of the last century blues players. More recently, the fairly ancient open G tuning went to multi platinum global fame yet again through composer and guitarist Keith Richards with the Rolling Stones, who readily testifies about how his songwriting was epiphany effected after getting hip to the open 'G' twisting of the pegs. |
|
And if you just plain love to rock out loud with your guitar, you owe it to yourself to retune your git and dive into any of riffs and patterns that motors any one of the many wonderful songs that Mr. Richards conjured up for us. And maybe like his epiphany, in minutes you realize a whole new universe of possibilities, one that brings a lot of fun and surely tradition, as its history roots go very deep and BLUES into the music of Americana. It's amazing how in just rooting around in these open tunings that oldtime cliche licks reveal themselves. |
This 'open tuning epiphany' personally happened twice for me. First with the open tuning taught to me as the 'Hawaiian 6/9', during a slide guitar lesson. The second was with the open 'G' when playing old time blues. If yet another reason was needed to justify having two or even three serviceable guitars, surely having rigs for standard, open 'G' and 'D' tuning could be near the top of the list :) Composers should take note here as open tunings often help discover new combinations, which can be adapted to standard tuning or not, depending. |
Tuning up a guitar from scratch. This first tuning is probably the most common, arranging the pitches in what is often termed 'standard' or 'concert' tuning. Here are the open string letter name pitches. This twisting of the pegs is most common and works in a wide range of settings. Everything from honky tonks to concert halls. In this method of tuning up one way we can get our starting pitch / tone by using a tuning fork created to sound 'A' ~ 440.
Tap the fork to get it ringing. Tune up the 'A' string on your git to match this pitch. Pop the 'A' string's harmonic at the 12th fret to double check your 'in tune-ness.' Listen for the waves between the notes. When there's no waves or warble in the notes together, they be in tune :) We theory cats would call it a unison. If there's a piano nearby, this pitch also corresponds to the 'A above middle C.' Strike the key and sustain it and match its pitch with the 5th string, we then can tune the rest of the strings from this starting pitch. If you already know the string names this is a breeze. If not, then rote learn the six of them now and you can be done with once and for all. Here's the method. First time is always tricky so be patient with yourself please :) 1) tune up the 5th string A, open or at the harmonic at the 12th fret to the pitch of the struck fork. 2) find the pitch A at the 5th fret of the low E string and match it up with the open A 5th string. 2a) or tune the low E string to its octave E above, located at the 7th fret of the A string. 3) find the D on the 5th string / 5th fret and tune up the open 4th string D. 4) find the G on the 4th string / 5th fret and tune up the open 3rd string G. 5) find the B on the 3rd string / 4th fret and tune up the open 2nd string B. 6) find the E on the 2nd string / 5th fret and tune up the open 1st string E. You should be out of strings now :) Play your favorite chord and decide if it sounds ok. Tweak the strings as needed. Using the 'E' maj / min and 'G' open chords is common for this as the guitar historically is designed around these pitches and their relative key centers. Also, most of the above method works by matching the pitches of adjacent string harmonics between the 5th and 7th frets. Use the the above open strings for tuning the G and B strings. |
|
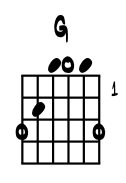
Open G. The first of our open tunings here is open G. Here we simply tune the open strings to sound a G major triad / chord. As this is also a common tuning for the five string banjo, tis easy to imagine the historical transfer of the tuning from banjo to guitar in our early Americana days. That it makes a super rocking chord machine out of any guitar with a ton of blues in the middle strings as well makes it just a hoot and a holler ... but that's banjo talkin' I'd imagine and we are theorists :) Regardless, going from standard to concert is a breeze. If your ax is tuned up to standard, un-twist each of the strings to get to the open G magic. Oh, the B string stays the same so ... Banjo's traditionally are four or five strings right? So ... leave off the low 6th string for a brighter sound. On any thing with any sort of a tune-a-matic bridge, easy to loosen the string and just set it out of the way. Historically speaking this open G was a 'gamechanger' for Keith Richards when he first learned it. No surprise then that a dozen or so global hits for band followed. |
|
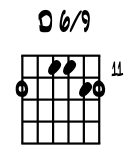
Hawaiian 6 / 9. The next open tuning is a jammer's delight. While taking a lesson with this blues cat Mario, it never went further, much to my later own chagrin, for once we tuned up to play some slide with these pitches, the lesson ended for me. For true be told a whole new universe of coolness immediately opened right up. Hope you have as magical a moment. Here are the pitches evolved from concert. So why 6 / 9? well, those are the two colortones added to the three note triad. Great slide key, such as Hawaiian slack key styles ( ? ) and there must be some blues in here too. I wish now I had stuck around for more, although did write a suite of tunes based in this tuning. |
|
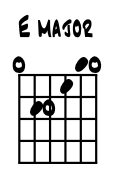
Open E. The next open tuning is very much like the open G above but based on E. This is perhaps more of a slide key than the other two as it tunes right into the standard or concert tuning with no transposition thus mixes in better with standard tuned instruments. Examine the pitches. Open E was a favorite slide key of Duane Allman. Alaskan blues master Joey Fender concurrs, helps in visually locating himself on the bandstand with other guitar / bass players. |
|
For the vocalist and totally just saying ... One of the last things that science has yet to discover is how and if a singing voice is effected when it is accompanied by a guitar tuned to an open tuning versus an standard tuned guitar. For example, in the open G chord included here, there are three G notes that range two octaves. If the melody note being sung is G, how much variability is there in pitch in the voice? Is the voice coerced into this pitch and does that effect its emotional statement? |
|
Does this really matter? Not being a singer I do not know. That said, when I listen to singers who play this chord and sing along, their vocal pitch seems 'determined' by their instrument and sounds 'dull' in regards to artistic coloring. So I muse ... if a voice had to work a bit harder to find their pitch in the mix of an open tuning would there be a more colorful pitch and sound created ...? |
|
Three favorite singers; Joni Mitchell, Muddy Waters and Bob Dylan seem to a have a wider variety of pitch as they go through their verses in songs. In Ms. Mitchell's case, open tunings are a part of her composition. Mr. Waters is a bluesman, so there's all sorts of interpretive nuances. Mr. Dylan just seems to be telling his story and honestly, it's hard to convincingly play his melody lines as single note guitar melodies. Again, just saying here as I be a terrible terrible singer ... but sure do love to hear a singer's stories :) So for the vocalist reading here, try an open tuning sometime, even just to see where it might take your most cherished melody lines and the stories they tell. |
|
That's all for this first chapter folks. Not really sure if we needed to go this far into all this tuning but it is an interesting story spanning mucho millennia. Knowing that to build chords we need a mathematically tighter system than for our original melody pitches in a sense mirrors the theory relationship we often find in our Americana musics. |
Ideally, by understanding how our musical system of pitches is created and tuned and how we build that structure into our guitars provides us with; another basis and way into understanding whatever music might come our way, a perspective of the raw source materials and how they are built into art, help us imagine new ways to organically build new ideas into our existing system. |
We also can gain a sense of what makes a good instrument and why it is worth having. That as our ears evolve and better understand what we hear, we can hear the virtues of an instrument that just may help better realize our own ideas as well as inspire us to push beyond existing forms and boundaries etc. |
Review and quiz. Our modern Americana six string guitar has many ancestors from many cultures. Its tuning we can reasonably trace to the later Renaissance of Florence, Italy. Here we find Vincenzio Galilei, an accomplished performer and composer for the lute. We credit Mr. Galilei with recording for posterity what was then called the 'rule of 18', original source unknown (?), which properly laid out the fret spacing on the lute to achieve an equal temperament of tuning of the 12 half steps within the octave. Successive generations of builders refined this rule as newer methods of building and measuring were discovered. Standardizing classical guitar construction began in the early 19th century in Spain, and traveled West to the New World of Mexico, then making it's way north up through to Texas, where it meets Banjo and our own Americana string traditions begin. And from that point forward our instruments have been nearly identical in how the frets are positioned and thus, the pitches they create and how we love to tune 'em on up. |
|
|
|
"If I fail I'll face it, but I can't live with not trying." |
Jonathan Bender New York Knicks 2009 |
“That’s why I’m here, and what pushed me to get here is the people who doubted me, I always have to keep that.” |
wiki ~ Austin Reeves |
References. References for this page's information comes from school, books and the bandstand and made way easier by the folks along the way. |
Find a mentor / e-book / academia Alaska. Always good to have a mentor when learning about things new to us. And with music and its magics, nice to have a friend or two ask questions and collaborate with. Seek and ye shall find. Local high schools, libraries, friends and family, musicians in your home town ... just ask around, someone will know someone who knows someone about music and can help you with your studies in the musical arts. |
|
Always keep in mind that all along life's journey there will be folks to help us and also folks we can help ... for we are not in this endeavor alone :) The now ancient natural truth is that we each are responsible for our own education. Positive answer this always 'to live by' question; 'who is responsible for your education ... ? |
Intensive tutoring. Luckily for musical artists like us, the learning dip of the 'covid years' can vanish quickly with intensive tutoring. For all disciplines; including all the sciences and the 'hands on' trade schools, that with tutoring, learning blossoms to 'catch us up.' In music ? The 'theory' of making musical art is built with just the 12 unique pitches, so easy to master with mentorship. And in 'practice ?' Luckily old school, the foundation that 'all responsibility for self betterment is ours alone.' Which in music, and same for all the arts, means to do what we really love to do ... to make music :) |
 |
"These books, and your capacity to understand them, are just the same in all places. Always bear in mind that your own resolution to succeed, is more important than any other one thing." |
|
Academia references of Alaska. And when you need university level answers to your questions and musings, and especially if you are considering a career in music and looking to continue your formal studies, begin to e-reach out to the Alaska University Music Campus communities and begin a dialogue with some of Alaska's finest resident maestros ! |
~ |
| Footnotes: |
| A(5) These designations pitch come from the 88 piano keyboard. The pitch A(4) @220 Hz., is below middle C known as C4, while the pitch A(5) @ 440 Hz., corresponds to the A above middle C on the standard 88 key piano keyboard. Reblitz, Arthur A. Piano Servicing, Tuning and Rebuilding, p. 206. Vestal Press, Maryland. 1993. |
| (1) Mike Doolin / mike@DoolinGuitars.com / Mr. Doolin took the time to explain this essential component and word the fret placement / tuning problem so eloquently to me by e-mail. |
| (2) The "12th root of 2." Reblitz, Arthur A. Piano Servicing, Tuning and Rebuilding, p. 206. Vestal Press, Maryland. 1993. |
| (3) Isacoff, Stuart. Temperament ... The Idea That Solved Music's Greatest Riddle, p. 162-163. USA Alfred A. Knopf, New York. 2001 |
| (4) Isacoff, Stuart. Temperament ... The Idea That Solved Music's Greatest Riddle, p. 210-212. USA Alfred A. Knopf, New York. 2001 |
| (5) Denyer, Ralph. The Guitar Handbook, p. 42. Great Britain. Pan Books, London. 1982 |